2장. Mathematical Background

In this chapter we will review the essential mathematical concepts, definitions, and properties required for the formal description of bilinear pairings.

이번 세미나는 2장. Mathematical Background의 2.1.2 subgroup까지 다룹니다.

암호화 관련 세미나를 하다보면 대부분의 참석자들이 수학적 장벽에 부딪혀 포기하는 것을 봅니다. 여차여차해서 우회하도록 안내하기는 하지만 여간 찜찜한게 아닙니다. 아무래도 안 되겠다 싶습니다. 이번 세미나는 좀 느리게 가더라도 최소한 추상대수에 대한 강의 하나 정도는 끝내고 가려고 합니다. KOCW에 올라와 있는 국민대학교 이옥연 교수님의 현대대수학을 2장 주제와 함께 수강하는 것으로 해서 진도를 맞추도록 하겠습니다.

이번 세미나에서는 5번 항목까지 수강하는 것으로 하겠습니다. 매일 세 개의 강좌를 들어야 하니 계획을 잘 세우고 진행하시기 바랍니다.

수강을 마치고 본문 내용을 한 번 읽고, 아래 요약한 내용을 다시 한 번 읽어 봅니다.

2.1 Algebra

2.1.1 Group

• 공집합이 아닌 이항 연산자 *에 대해 다음을 만족하는 것을 군이라고 합니다.
  • *에 대해 닫혀 있어야 합니다.
  • 항등원(identity)과 역원(inverse)이 존재해야 합니다.
    • Each element of G admits a (unique) symmetric (also called its inverse)
  • 결합법칙이 성립해야 합니다.
• 교환 법칙이 성립할 때의 군을 아벨군이라고 합니다. 이 책에서 다루는 대부분의 군은 아벨군입니다.
• 군은 하나에 연산에 대해서만 정의합니다. 연산은 덧셈이거나 곱셈일 수 있습니다.
  • 덧셈인 경우 항등원은 0, a에 대한 역원은 -a입니다.
  • 곱셈인 경우 항등원은 1, a에 대한 역원은 a^-1입니다.
• G의 원소 갯수를 위수(order)라 합니다.
  • 위수가 유한 개 일 때 유한군이라고 합니다.
• G의 원소 g에 이항 연산을 r-1번 적용했을 때 e가 되게 하는 가장 작은 r을 원소의 위수(order of group element)라 합니다.
  • _*^r(g) = e
    • 예를 들어 (G, +) 군에 속하는 원소 g의 위수가 3이라면 g + g + g = 0이 된다.
• 군 중에는 군의 원소 g에 이항 연산을 거듭 했을 때 군의 모든 원소를 생성할 수 있는 것들이 있습니다. g를 생성원(generator)라고 하고, 적어도 하나의 생성원을 갖는 군을 순환군(cyclic group)이라고 합니다.
  • G = <g>라고 표현합니다. 모든 순환군은 아벨군입니다.
• 유한군의 위수가 소수 p이면 p-1개의 생성원을 갖습니다. 항등원을 제외한 모든 원소가 생성원이 됩니다. 
  • σ(n)는 생성원의 갯수를 나타냅니다. σ(p) = p-1
• 덧셈 군의 연산은 +로, 항등원은 0으로, a의 역원은 -a로 표현합니다. a에 + 연산을 m – 1 번 반복하는 것은 ma로 표현합니다. 양의 정수 n을 나누는 수(modulo)로 나머지 연산한 유한 집합은 Z_n = {0, 1, . . . , n − 1}으로 표현하고, 덧셈 연산이 적용될 때 (Z_n, +)로 표현합니다.
• 곱셈 군의 연산은 ×로, 항등원은 1로, a의 역원은 a^-1로 표현합니다. a에 × 연산을 m − 1 번 반복하는 것은 a^m으로 표현합니다. Z_n의 원소들 중에서 0을 제외하고 n과 약수가 1뿐인(n에 상대적인 소수) 원소들로만 이루어진 집합을 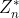으로 표현하고,  곱셈이 적용될 때 (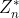, ×)로 표현합니다.
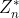  • (, ×)는 σ(n)인 아벨군입니다. 
    • 
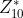
      • n이 10일 때 Z_n = {0, 1, 2, 3, . . . , 9}, 여기서 0을 제외하고, 10과 약수가 1뿐인 것은 {1, 3, 7, 9}
        • 3과 7을 생성원으로 갖는 순환군
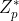  • (, ×, 1)는 위수가 p – 1인 유한 순환군입니다.

2.1.2 Subgroup

• 군의 부분집합 중 군이 되는 것을 부분군(subgroup)이라고 합니다.
• G가 아벨군이고 m이 정수일 때 G{m} = {a ∈ G | _*^m(a) = e}는 G의 부분군이 되고, (G{m}, *)로 표현한다.
• G가 유한 아벨군이고, H가 G의 부분군일 때 H의 위수는 G의 약수가 됩니다.
  • 예) (,  ×)
    • 위수가 12인 아벨군
    •  = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
      • {2} = {1, 12}
        • Z₁₃에서 a²했을 때 1이 되는 것
        • ×에 대한 항등원은 1
        • 13으로 나머지 연산
      • {3} = {1, 3, 9}
      • {4} = {1, 5, 8, 12}
      • {5} = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
      • {6} = {1, 3, 4, 9, 10, 12}
      • …
    • 이들이 군임을 알 수 있고, 부분군임을 알 수 있습니다. 부분군의 위수가 군의 위수의 약수가 됨을 알 수 있습니다.
• G가 아벨군이고 m이 정수이고, _*^m(G) = {_*^m(a) | a ∈ G} 일 때,  (_*^m(G), *)는 G의 부분군이 됩니다.
  • 예) 아벨군 (,  ×)에서 m이 9이면
    • ()⁹ = {a⁹ | a  ∈ } = {1, 5, 8, 12}
    • ()² = {1, 3, 4, 9, 10, 12}
    • ()³ = {1, 5, 8, 12}
    • ()⁴ = {1, 3, 9}
    • ()⁵ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
    • ()⁶ = {1, 12}
  • 이전 예와 비교해 보면
    • ()⁴ = {3}
    • ()³ = {4}
    • ()⁶ = {2}
    • ()² = {6}
      • (G, ×)의 위수가 c × r로 인수분해 되면, {a^c | a ∈ G} = {a ∈ G | a^r = 1}
      • (G, +)이면, {ca | a ∈ G} = {a ∈ G | ra = 0}